Historia de la Ciencia de datos
Aunque a día de hoy podemos ver multitud de menciones en medios de comunicación o un incremento en la oferta de puestos de trabajo relacionados con el análisis de datos como "data analyst", aunque la falta de una terminología clara y universalmente aceptada, hace que también sea frecuente observar otros como "data sciencits", "big data", "data sience" y un sinfín de nombres que generan mucha expectación y hype, pero la realidad es que los seres humanos llevamos, prácticamente, analizando información y recopilando datos toda nuestra historia.
El primer vestigio de la recopilación de datos se remonta al 18.000 a.C, con el Hueso de Ishango, que muestra muescas utilizadas por tribus paleolíticas para registrar suministros y actividades comerciales.

Más tarde, el ábaco surgió en la antigua Babilonia como la primera herramienta dedicada exclusivamente a los cálculos.

En el 100-200 d.C., los científicos griegos construyeron el Mecanismo de Anticitera, considerado el primer ordenador mecánico, utilizado para registrar ciclos olímpicos y el seguimiento astrológico.
El surgir de la estadística, también marcó un punto de inflexión, en 1663 John Graunt realizó el primer experimento de análisis de datos en Londres, registrando información sobre la mortalidad con la hipótesis de crear un sistema de alerta temprano para la Peste.
En 1880, la invención de la Máquina Tabuladora de Hollerith revolucionó el procesamiento de datos, reduciendo el retraso de una década de la Oficina del Censo de EE. UU. a solo unos meses mediante el uso de tarjetas perforadas.
A partir de este punto, empezaron a nacer los conceptos modernos de almacenamiento de datos, especialmente a partir de 1920, siendo en 1928 cuando el ingeniero germano Fritz Pfleumer ideó el almacenamiento magnético en cinta, que todavía a día de hoy es utilizado en discos duros.
Décadas después, en 1965 el gobierno de EE.UU. planificó el primer centro de datos a gran escala y en 1970 se inventó la base de datos relacional por el matemático de IBM Edgar Codd, cuyo marco sigue siendo fundamental en servicios de datos contemporáneos, permitiendo a los usuarios consultar datos con SQL.
El término "Big Data" fue utilizado por primera vez por Erik Larson, coincidiendo con el creciente interés en el Business Inteligence y el uso de nuevos sistemas y Software para rastrear el rendimiento empresarial.
El impacto en el Marketing, por supuesto, ha sido dramático, desde la publicidad impresa en 1450, el Marketing siempre se ha centrado en la difusión masiva.
La llegada de los medios de difusión (radio, televisión) forzó a los especialistas en Marketing a gestionar múltiples canales y buscar comprender al consumidor más allá de los mensajes genéricos.
La tecnología digital, los canales de difusión como las redes sociales han transformado el Marketing más tradicional, la era digital permite ver a los especialistas y profesionales las interacciones de los consumidores y el público más rápidamente.
Hoy, el análisis de datos sigue evolucionando a un ritmo frenético, impulsado por la irrupción de la Inteligencia Artificial y el aprendizaje automático, la dificultad reside en cómo manejar, interpretar y utilizar los datos y qué profesionales saben realmente utilizar las diferentes herramientas disponibles para su arsenal.
¿Qué es la ciencia de datos o el Data scientist?
Como hemos visto, en la era digital el análisis de datos para empresas o profesionales de diferentes sectores no es una ventaja competitiva, es fundamental una comprensión profunda del campo y de las herramientas.
Pero primero deberíamos preguntarnos: ¿Qué es la ciencia de datos?
Como mencionamos anteriormente, hay mucha expectación y hype alrededor del análisis de datos, es frecuente ver constantemente menciones a puestos de "data analyst", o términos ambiguos y poco definidos como "big data" o "data science".
Esta falta de una definición concisa sobre la terminología básica supone un claro problema, por ejemplo, ¿Qué es la Big data?, cuando hablamos de "big", ¿Cuánto es realmente "big"?.
Otra pregunta que podría surgirnos es, ¿Qué relación tiene la Big data con la ciencia de datos?, aunque ciertamente podríamos suponer que mucha gente quizás asocia la "ciencia de datos" a tareas complejas que se realizan en compañías tecnológicas famosas como Google, Facebook y similares.
En realidad, parece ser que el término "data scientist" fue acuñado en 2008 por DJ Patil y Jeff Hammerbacher en Linkedin y Facebook, para "describir" un nuevo tipo de rol.
Se podría decir que, el data scientist sería una mezcla de "hacking" (Ingeniería de software) y estadística y el profesional posee un conocimiento práctico de herramientas y materiales con la comprensión teórica de lo que es posible con los datos, pero como digo, existe una falta de una definición concreta y el debate continua y es más extenso y profundo de lo que aquí se refleja.
Fundamentos del Análisis de datos e Inferencia estadística
El análisis de datos en la era de Big data se inicia con una comprensión profunda del pensamiento y la inferencia estadística.
Aunque el término "Big data" es amplio y como hemos dicho carece de una definición estandarizada, representa no sólo un conjunto de tecnologías y una revolución en la medición, sino también una nueva filosofía para la toma de decisiones.
El mundo que nos rodea es inherentemente complejo, aleatorio e incierto, pero a su vez, es una gran máquina generadora de datos.
Cada aspecto de nuestra vida, desde nuestras interacciones online hasta los procesos biológicos internos, producen rastros de datos.
El "data scientist", o el científico de datos como observador, transforma el mundo de datos mediante métodos de recolección o muestreo, un proceso que inherentemente es subjetivo, lo que introduce dos fuentes de incertidumbre: la aleatoridad del proceso en sí y la incertidumbre de la recolección de los datos.
La inferencia estadística es la disciplina que nos permite extraer significado e información de esos datos generados por procesos aleatorios.
El objetivo es claro: simplificar esos vastos rastros de datos en algo más comprensible, como modelos matemáticos o estimadores estadísticos, para poder entender y describir los procesos del mundo real y tomar decisiones.
Población, muestra y desafíos del Big Data
En la estadística clásica se distingue entre población (el conjunto completo de objetos o unidades, no solo personas) y muestra (un subconjunto de esa población que se examine para sacar conclusiones sobre el total), por lo que es importante mencionar que la forma en la que se selecciona la muestra es crítica, ya que un muestreo sesgado puede distorsionar las conclusiones.
En la era del Big Data, surge un pregunta interesante: si podemos registrar "todo" (N=ALL), ¿siguen siendo relevantes los conceptos de población y muestra?
La respuesta es que sí, incluso con grandes volúmenes de datos, el muestreo sigue siendo una solución para desafíos computacionales y, crucialmente, la mayoría de los "Big Data" no son realmente "todo".
Además, los sesgos en la recolección de datos son omnipresentes; por ejemplo, un análisis de los tuits durante una catástrofe podría subestimar la magnitud de la devastación al solo captar la perspectiva de los usuarios activos en Twitter (o X) que aún pueden publicar post.
Los modelos en Ciencia de Datos
Un modelo es un intento de entender y representar la realidad a través de una lente particular, abstrayendo o eliminando detalles superfluos.
En estadística y ciencia de datos, los modelos son funciones matemáticas que captura la naturaleza de los procesos generadores de datos, con parámetros que se estiman a partir de la información.
La construcción de un modelo es tanto un arte como una ciencia, y a menudo se comienza con la exploración de datos (EDA) y la formulación de supuestos simples, construyendo la complejidad gradualmente.
Las distribuciones de probabilidad (como la normal, Poisson o exponencial) son los cimientos de los modelos estadísticos, describiendo la forma empírica de las mediciones de los procesos naturales.
El proceso en Ciencia de Datos
El proceso de ciencia de datos suele encajar en el marco general que se muestra en la siguiente imagen.
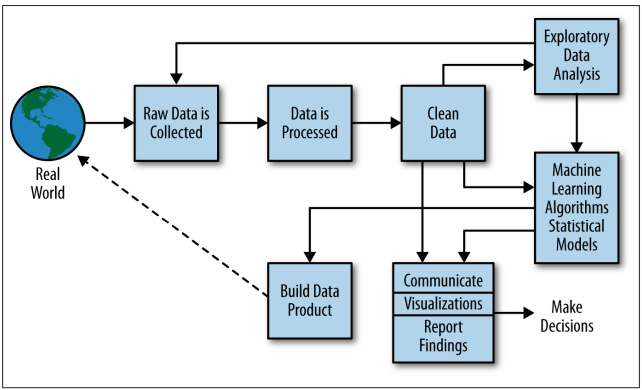
En primer lugar tenemos el mundo real que, como habíamos dicho, es un gran generador de datos.
En el mundo real, hay personas utilizando Youtube, otras personas realizando Podcast y multitud de gente recibe diferentes pruebas médicas a lo largo del día.
Todas estas actividades, generan datos, por lo que empezaremos con "Raw Data", que deberán ser procesados para que puedan ser aptos para ser analizados, por lo que se pueden crear y utilizar pipelines para data munging (transformación y mapeo de datos): unión, raspado o manipulación de datos.
Para dicho fin, podremos utilizar herramientas como Python (Pandas y NumPy), scripts de Shell, R o SQL, o todas las anteriores y nuestros datos tendrán un formato más compatible con un análisis posterior y más entendible, como podemos observar en el siguiente ejemplo visual:
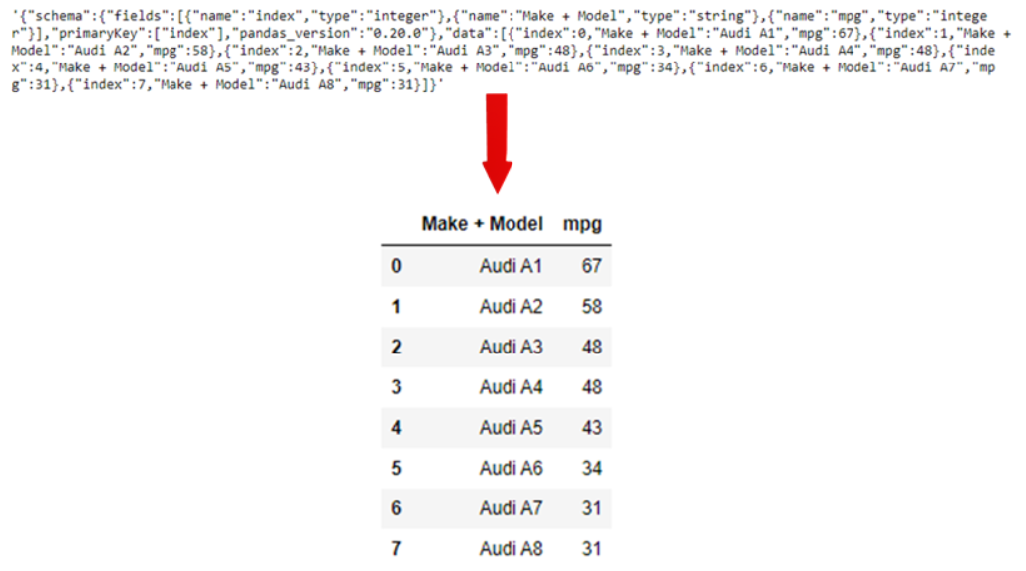
Una vez que los datos estén en un formato más limpio, se puede empezar con un análisis exploratorio de los datos (EDA).
En esta situación, es habitual darse cuenta de que, en ocasiones, nuestra dataset no está "tan limpia", ya bien sea porque hay duplicados, faltan algunos valores, algunos datos no son consistentes con lo esperado o incluso los datos no se han introducido correctamente, por lo que es habitual tener que volver a un punto anterior del proceso para recopilar más datos o trabajar más la dataset.
A partir de este punto, diseñamos un modelo para usar un algoritmo como el de k vecinos más cercanos (KNN), la regresión lineal, Naive Bayes (NB) u otras opciones y su elección dependerá del tipo de problema que trata de resolverse: un problema de clasificación, un problema de predicción o un problema de descripción básico, por ejemplo.
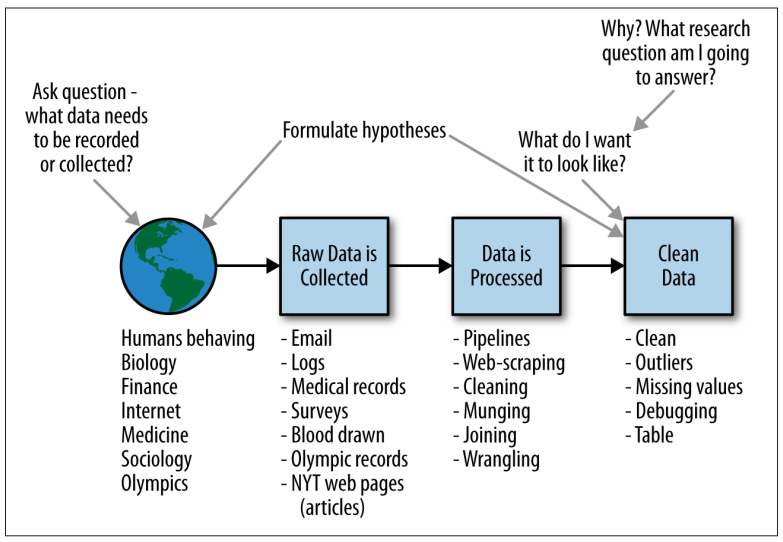
Posteriormente, podremos interpretar, visualizar y reportar o comunicar los resultados, por lo tanto un profesional que trabaje en este proceso estará involucrado en todas las partes del proceso, como podemos observar en la siguiente imagen y que es una variación del método científico:
El profesional que realice el proceso estará involucrado prácticamente en todas las fases, con diferentes objetivos.
Algoritmos
Un algoritmo es un procedimiento o un conjunto de pasos o reglas para lograr una tarea.
Son uno de los conceptos más fundamentales, o bloques de construcción, de la informática:
Los algoritmos son uno de los conceptos fundamentales, o bloques de construcción, de la ciencia de la computación: la base del diseño de código eficiente, la preparación y el procesamiento de los datos y la ingeniería de Software.
Los tipos básicos de tareas que los algoritmos pueden resolver son la ordenación, la búsqueda y los problemas computacionales basados en grafos.
Una tarea determinada, como ordenar una lista de objetos, podría ser manejada por múltiples algoritmos posibles, existe una noción de "mejor" medida por la eficiencia y el tiempo computacional, lo cuál es especialmente importante cuando se trata de grandes cantidades de datos y se construyen productos para el consumidor.
Los algoritmos que funcionan de forma secuencial o en paralelo son la base de los pipelines para procesar y preparar los datos.
En relación a la ciencia de datos, hay al menos tres clases de algoritmos de las que uno debe ser consciente:
Algoritmos de Machine Learning
Los algoritmos de aprendizaje automático se utilizan, en gran medida, para predecir, clasificar o agrupar (clusterizar).
Es crucial entender que el Machine Learning (ML) no es una disciplina aislada, es, de hecho, un subcampo de la Inteligencia Artificial (IA) y una extensión natural de la estadística.
Los potentes algoritmos que impulsan productos de datos esenciales, desde el reconocimiento de voz hasta la clasificación de contenido, están fundamentados en principios estadísticos robustos.
Contrario a percepciones pasadas, los programas de estudio y departamentos de estadística ahora integral el Machine Learning como una parte central e indispensable.
Esta integración subraya que, si bien la IA es el campo amplio que busca emular la inteligencia humana, el Machine Learning es una de sus herramientas más poderosas y omnipresentes, profundamente arraigada en metodologías estadísticas.
Hay algunos puntos que se pueden considerar:
Regresión lineal
Uno de los métodos estadísticos más comunes es la regresión lineal.
En su forma simple, se utiliza para expresar la relación matemática entre dos variables o atributos.
Se asume que existe una relación entre una variable de resultado (a veces llamada variable de respuesta, variable dependiente o label) y un predictor (a veces también llamado variable independiente, variable explicativa o feature).
Asumir que existe una relación lineal entre una variable de resultado y un predictor es una suposición grande, pero también es una de las más simples que se puede hacer, por lo que generalmente es un buen punto de partida.
En algunos casos, tiene sentido que los cambios en una variable se correlacionen linealmente con los cambios en otra variable.
Por ejemplo, tendría sentido que cuantos más helados vendas, mas dinero ganes, por lo que la suposición de linealidad es más asumible.
En otras ocasiones, la suposición de linealidad es más difícil de justificar.
¿Por qué construir un modelo lineal?
El interés de construir un modelo lineal reside en utilizar esta relación para predecir resultados futuros o, que quieras comprender o describir la relación para tener una idea más clara de la situación.
Aplicado al marketing, supongamos que se está tratando de estudiar la relación entre las ventas de una empresa y lo que están gastando en publicidad, o cuánto dinero gasta de media un cliente en una página web y la duración de la sesión.
Estos resultados, son numéricos, lo que significa que la regresión lineal es una elección acertada, al menos, para un primer acercamiento.
Ejemplo hipótetico Nosoyvisible
Consideremos un caso hipótetico de "nosoyvisible.com", donde estamos probando con campañas nuevas de publicidad.
En el experimento inicial controlado, observamos que por cada 100 euros invertidos en publicidad, el sitio web recibía consistentemente 500 visitas adicionales.
Si registramos los datos de las campañas y se los mostramos a alguien podrán observar que hay un claro patrón, podríamos expresarlo como una serie de puntos:
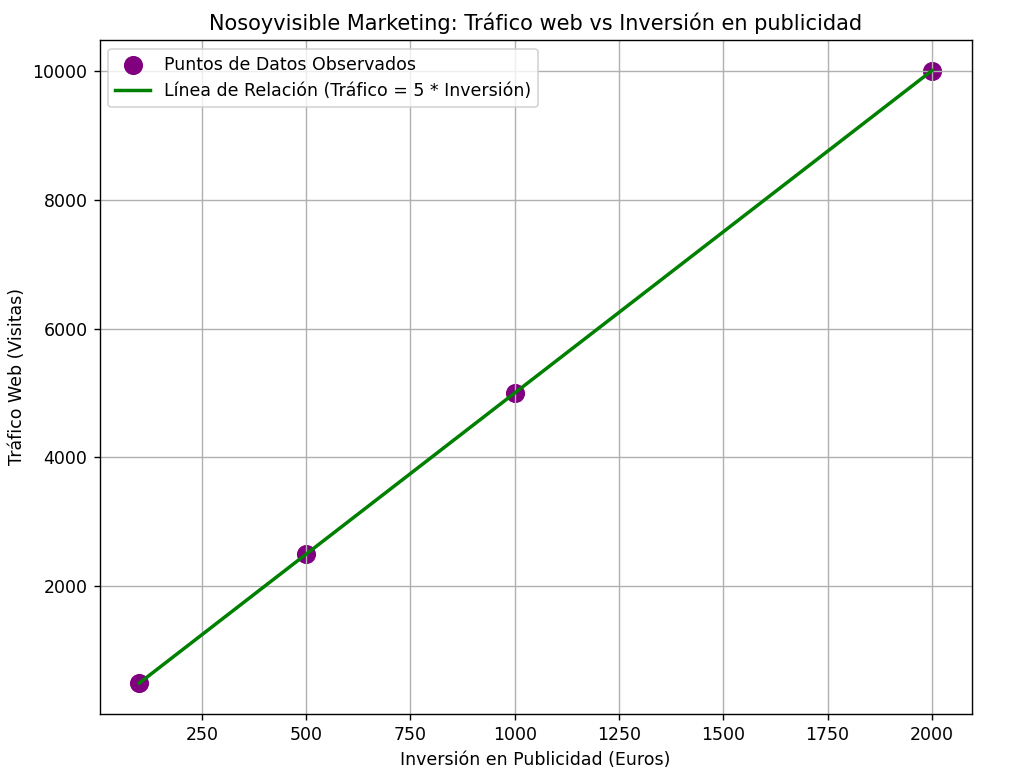
S={(x, y) = (100, 500), (200, 1000), (500, 2500), (1000, 5000), (1500, 7500), (2000, 10000)
Como podemos observar arriba, existe un patrón lineal determinista con un coeficiente entre x e y de 5.
INVERSIÓN EN PUBLICIDAD | TRÁFICO WEB (VISITAS) |
|---|---|
100 | 500 |
200 | 1000 |
500 | 2500 |
1000 | 5000 |
1500 | 7500 |
2000 | 10000 |
Podríamos, incluso, representarlo con Python:
Datos a nivel de Usuario: Ejemplo más realista
Dejando atrás el escenario tan idealista del ejemplo anterior, ahora nos adentramos en los datos que Nosoyvisible ha recopilado.
Tenemos un conjunto de datos detallado, donde cada fila corresponde a un usuario único de nuestra plataforma digital y las columnas registran su comportamiento durante una semana, donde asumiremos que los datos ya han pasado por un proceso de limpieza y preparación, donde tenemos acceso a un volumen importante de información, de una magnitud suficiente.
Entre las columnas de este dataset, encontramos métricas cruciales para nuestro negocio, como por ejemplo interacciones_clave_semana (que incluiría eventos específicos), duración_sesion_segundos, numero_visitas, anuncios_mostrados, edad_usuario, genero_usuario y otras variables de comportamiento de interés.
Utilizamos una muestra aleatoria de 100 usuarios y nuestro interés principal sería entender cómo se relacionan ciertas variables.
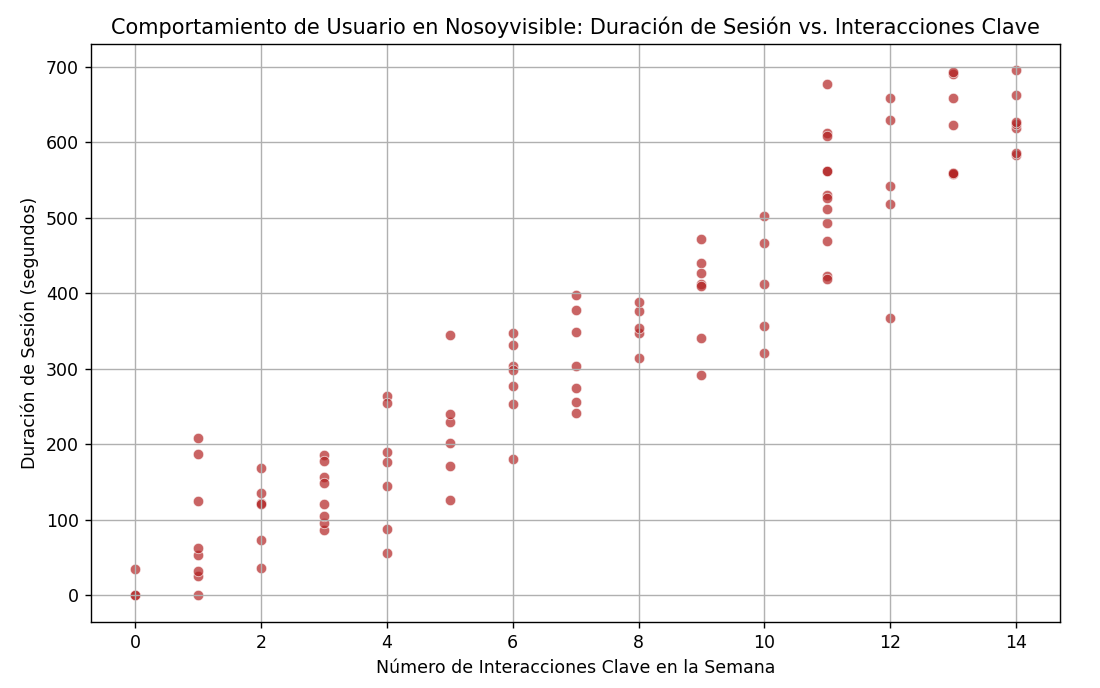
Por ejemplo, podríamos graficar interacciones_claves_semana (x) frente a duracion_sesion_semana (y).
El objetivo, podría ser claro: podríamos ofrecer, en el caso de que existieran a nuestros anunciantes un pronóstico fiable sobre el volumen de usuarios o el nivel de engagement que pueden esperar.
También, podríamos comprender los factores que influyen en duracion_sesion_segundos que es un paso crítico para optimizar la experiencia de usuario y, por ende, el valor que ofrecemos.
En contraposición al ejemplo idealista anterior, al observar las primeras filas de los datos muestreados (por ejemplo: 7 276, 3 43, 4 82, 6 136, 10 417, 9 269 en formato de interacciones - duración), rápidamente nos damos cuenta de que ya no somos capaces de discernir un patrón claro.
Los datos no siguen orden obvio y son demasiados para una inspección manual, por ello, volvemos a utilizar Python, y observamos:
Enter your text here...
Enter your text here...
k-Nearest Neighbors (k-NN)
Enter your text here...
Naive Bayes
Enter your text here...
Causalidad
Enter your text here...
Correlación no implica causalidad
Uno de los mayores desafíos a nivel estadístico, desde un punto de vista tanto teórico como práctico, es establecer una verdadera relación causal entre dos variables.
¿Estamos observando una mera asociación sin relación causal?
Responder a esta pregunta, aunque extremadamente importante y fundamental, es mucho más difícil de lo que puede parecer.
Aunque existen múltiples ejemplos, podemos mostrar que hemos descubierto una correlación entre la venta de helados y la venta de trajes de baño, observando los datos de ventas a lo largo del tiempo:
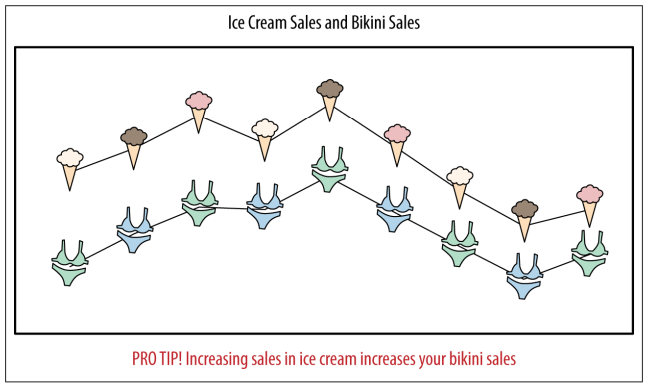
La asociación es clara entre las dos variables pero, evidentemente, no establece causalidad.
¿La gente se siente atraída a comer helado cuando usa un traje de baño?, ¿La gente se pone un traje de baño cada vez que come helado?
En realidad, la explicación es que hay una tercera variable, como el clima cálido que causa que la gente use más trajes de baño y también consuma más helados, la inferencia causal es el campo que se ocupa de comprender mejor las condiciones bajo las cuales una asociación puede interpretarse como verdaderamente causal.
Preguntas causales
El razonamiento y la forma de abordar una pregunta causal es: ¿Cuál es el efecto de x sobre y?
Algún ejemplo, podría ser: ¿Cuál es el efecto de este anuncio sobre el comportamiento del cliente? o, ¿Cuál es el efecto de un fármaco en la probabilidad de sufrir un evento cardiovascular? o, en el caso más general, ¿Cuál es el efecto del tratamiento en el resultado?
Estimar parámetros causales es difícil.
De hecho, la efectividad de la publicidad casi siempre se considera un punto discutible porque es muy difícil de medir.
La gente suele utilizar métricas de "éxito" porque son fáciles de estimar pero, en realidad, no miden lo que realmente quieren, a pesar de que todo el mundo toma decisiones basándose en ellas de todos modos porque, simplemente, es fácil.
Esto, tiene efectos negativos reales, los especialistas en Marketing terminan siendo recompensados por vender cosas en línea que de todos modos, se habrían vendido igual.
Ensayos clínicos aleatorizados
¿Cómo probar la causalidad?
El Gold standard para establecer causalidad es el experimento aleatorizado.
Es un método en el que asignamos aleatoriamente a un grupo de personas para que reciban un "tratamiento" y a otros para que estén en el grupo "control", es decir, que no recibirán el tratamiento y en su lugar recibirán una sustancia placebo.
Luego, tenemos algún resultado que queremos medir, y el efecto causal es simplemente la diferencia entre el grupo de tratamiento y el grupo de control en ese resultado medible.
La noción de usar experimentos para estimar los efectos causales, se basa principalmente en el supuesto estadístico de que el uso de la aleatorización para seleccionar dos grupos ha creado dos poblaciones que son "idénticas", desde un punto de vista meramente estadístico, equilibrando variables tanto conocidas como desconocidas que pueden influir en los resultados.
Es decir, como estamos tirando monedas, el resto de factores que podrían ser variables de confusión (la edad, fumador actual o en el pasado, la presencia o ausencia de enfermedades...) se "eliminan" o "cancelan", porque podemos garantizar que la edad, los fumadores y la presencia de enfermedades se distribuirán de forma uniforme entre las dos poblaciones, si se incluyen suficientes participantes en el experimento.
Como mencionamos, lo importante de la aleatorización es que ajusta los factores de confusión que conocemos, pero también nos dará un equilibrio en todas aquellas cosas que pueden influir en los resultados: todo lo que desconocemos.
Por supuesto, también existen limitaciones o problemas, sólo es ético realizar un ensayo clínico aleatorizado si la comunidad médica realmente no sabe qué tratamiento es mejor, es decir, no podemos asignar a las personas aleatoriamente para no recibir un medicamento, si sabemos que usar el medicamento será mejor para ellos que no darles nada.
Otro problema fundamental de los ensayos clínicos aleatorizados es que son muy caros y requieren de mucho trabajo, necesitando mucho tiempo y profesionales para que se ejecute de forma adecuada, aunque la alternativa de no realizar ensayos clínicos aleatorizados también puede llevar a suposiciones erróneas que son extremadamente costosas.
En definitiva, cuando son viables, los ensayos clínicos aleatorizados son el Gold Standard para dilucidar las relaciones de causa y efecto, aunque también existen otros acercamientos filtrando diferentes líneas de evidencia y utilizando los criterios de Bradford-Hilll, a pesar de que tienen limitaciones.
Average vs el individuo
Los ensayos clínicos aleatorizados miden el efecto de un determinado fármaco o una intervención promediado entre todas las personas.
A veces, se pueden agrupar a los usuarios para tratar de determinar el efecto promedio en hombres o mujeres, en personas de cierta edad o según la presencia o ausencia de diferentes patologías, pero en última instancia, los resultados son un promedio, por lo que no sabremos que sucede finalmente en un individuo.
Actualmente, existe un impulso y un interés creciente hacia la medicina personalizada con la disponibilidad de datos genéticos, es un cambio desde un enfoque donde observamos promedios a realizar inferencias sobre un individuo.
A/B Testing
En ciertos sectores o en las empresas de Software, lo que describimos como experimentos aleatorios sería el A/B Testing o pruebas A/B.
El concepto es bastante intuitivo y simple, de hecho, si la estructura está configurada correctamente, ejecutar un experimento puede reducirse a escribir un archivo de configuración corto y cambiar sólo un parámetro, ya sea un color, texto o diseño diferente o un algoritmo subyacente, que le da a algunos usuarios una experiencia diferente a la de otros.
Evidentemente, la ejecución de pruebas A/B en una empresa tecnología es mucho más fácil que la realización de un ensayo clínico y, por supuesto, hay menos en juego: no estamos tratando con la vida de las personas.
Otras detalles que marcan la diferencia es que no hay problemas de cumplimiento, en los ensayos clínicos aleatorios no podemos controlar si alguien toma el medicamento o no, mientras que en línea, podemos controlar totalmente lo que mostramos al usuario.
Evidentemente, esto es dependiente de si se configura correctamente la infraestructura experimental correctamente.
Se necesita algo de trabajo para configurarla bien y luego analizar correctamente los datos.
Además, cuando diferentes equipos de una empresa están trabajando en nuevas características de un producto o una página y todos quieren probar variaciones, si no se tiene cuidado, un sólo usuario podría experimentar múltiples cambios a la vez.
Por ejemplo, el equipo de UX podría cambiar el color o el tamaño de la fuente, o el diseño para ver si eso aumenta la tasa de clics mientras que, al mismo tiempo, el equipo de clasificación de contenido podría querer cambiar el algoritmo que elige qué recomendar a los usuarios, y el equipo de anuncios podría estar haciendo cambios en su sistema de pujas.
Supongamos que la métrica que nos importa es la tasa de retorno, y un usuario comienza a regresar más, sería difícil establecer la causa de la mejora en la métrica si se implementan múltiples cambios ya que había una falta de coordinación.
Estudios observacionales
Mientras el "Gold standard" generalmente se entiende que son los los experimentos aleatorizados o las pruebas A/B, no siempre son posibles, así que a veces nos conformamos con otra opción: los estudios observacionales.
Un estudio observacional es un estudio empírico cuyo objetivo es dilucidar relaciones de causa y efecto en los que no es factible, por múltiples motivos, utilizar la experimentación controlada.
Una gran parte de la actividad de la ciencia de datos gira en torno a los datos observacionales, aunque las pruebas A/B, como hemos mencionado, son excepciones a esa regla.
En definitiva, los estudios diseñados son casi siempre técnicamente mejores pruebas, pero hay muchos ejemplos donde no es ético realizarlos, o intervienen otros factores que dificultan su realización.
Enter your text here...
Paradoja de Simpson
Hay muchos problemas o limitaciones asociados a los estudios observacionales.
Observemos el siguiente gráfico, por ejemplo, donde se busca la mejor línea de ajuste para deducir si tomar dosis más altas de un medicamento "malo" se correlaciona con una mayor probabilidad de sufrir un ataque cardíaco.
Parece que, cuanto mayor es la dosis, menos ataques cardíacos sufre el paciente.
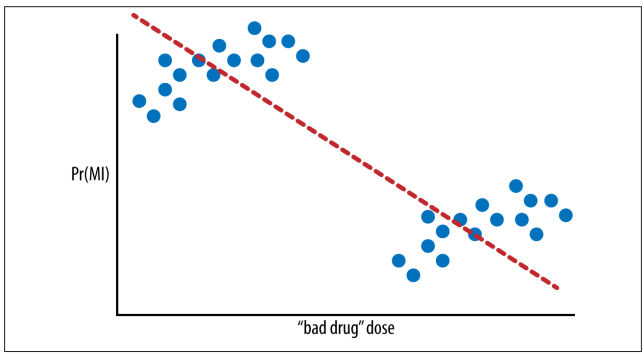
Probabilidad de sufrir un infarto de miocardio (MI) en función del tamaño de la dosis de un medicamento "malo".
Pero tenemos que tener en cuenta que, hay dos grupos, y si sabemos más sobre esos dos grupos, encontraremos la conclusión opuesta, como podemos observar en la siguiente figura.
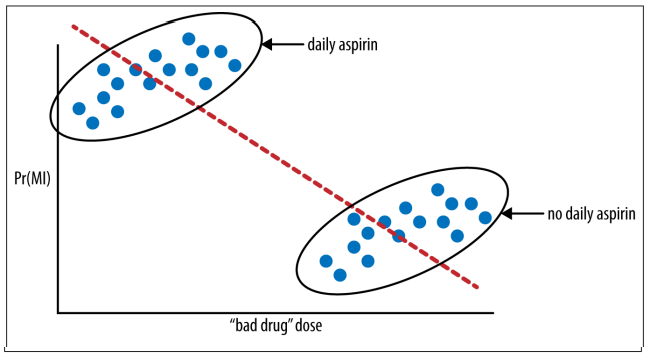
Probabilidad de sufrir un infarto de miocardio (MI) en función del tamaño de la dosis de un medicamento malo y si el paciente también tomó aspirina.
Evidentemente, esta imagen fue manipulada para que el problema fuera más claro pero, en el mundo real y cuando los datos son multidimensionales, sería muy difícil dibujar una imagen tan simple.
En este caso concreto, el consumo de aspirina es una variable de confusión, es decir, el consumo o no consumo de aspirina no se distribuyó aleatoriamente entre las personas del estudio y marcó una gran diferencia en el efecto aparente del medicamento.
Si pensamos en la línea original (primera imagen) como un modelo predictivo, en realidad sigue siendo la mejor opción que podemos obtener sin saber más sobre los hábitos de toma de aspirina o otras variables de confusión en los pacientes involucrados.
El problema aquí es que, estamos tratando de asignar causalidad, es un problema común con los modelos de regresión en estudios observacionales: una tendencia que aparece en diferentes grupos de datos desaparece cuando estos grupos se combinan, o viceversa.
Esto, se conoce habitualmente como la paradoja de Simpson.




